Bonjour et bienvenue dans Mathematica Hyrulea.

Vous avez peut-être eu la chance de tester les donjons d’Igor dans le tout nouveau Link’s Awakening. Dans ce mode, Igor nous fournit un ensemble donné de salles à assembler pour faire un donjon. Mais vous êtes vous déjà demandé combien de salles différentes vous pourriez créer, si vous en aviez le temps et les outils ? C’est ce que l’on va tenter de compter aujourd’hui.

 

I. Un peu de dénombrement :

Dans Link’s Awakening, les salles sont des rectangles de 8×6 cases. En simplifiant à l’extrême on pourrait dire que chaque case est soit un mur soit une case traversable. Dans les faits, il y a d’autres possibilités comme des vases, des torches, des trous, des tapis roulants, des coffres et j’en passe. Mais on va simplifier les calculs en se limitant à ces deux objets : mur et sol. Croyez moi, ça fait déjà beaucoup.

Faisons donc le calcul, il y a 8*6 = 48 cases. Chacune de ces cases peut être dans deux états différents : mur ou sol. Ce qui devrait donner 2⁴⁸ salles différentes. 2⁴⁸ c’est 2*2*2*…*2 avec 48 fois le nombre 2. Comment on sait ça ? C’est assez simple, laissez-moi vous montrer cet arbre. Quand on a une seule case, il n’y a que deux possibilités, on rajoute une deuxième case et cela multiplie par deux les possibilités, puis on en rajoute une troisième et on multiplie par deux de nouveau. Et ainsi de suite jusqu’à obtenir 2⁴⁸.

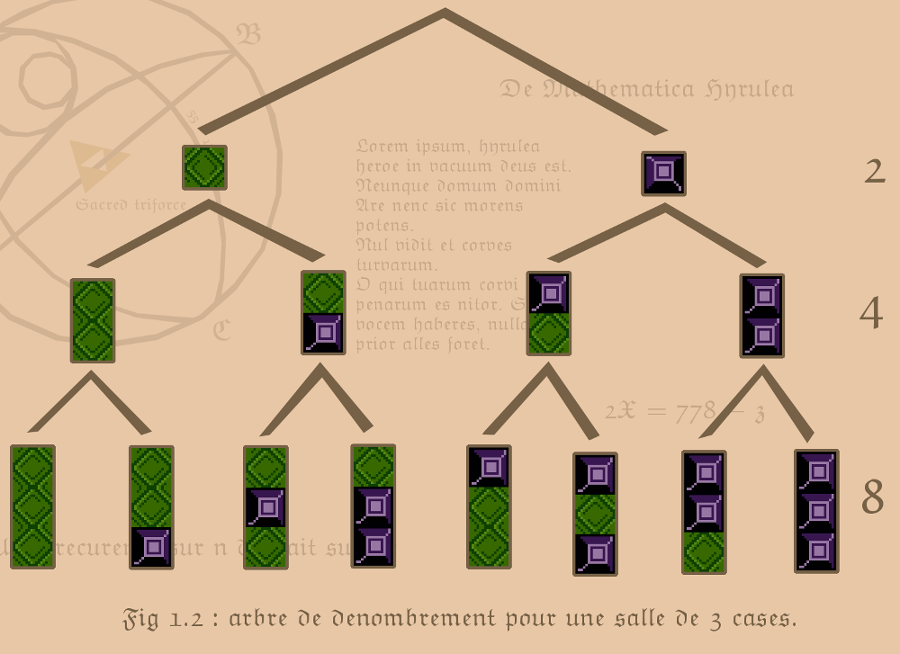
On pourrait croire que 2⁴⁸ est un petit nombre vu comme ça. Il ne prend que 3 chiffres à écrire. Et pourtant c’est un nombre un peu plus grand que 280 000 milliards. Même si vous parcourez chacune de ces salles en 10 secondes, il vous faudra 90 millions d’années pour visiter toutes les salles possibles. Il y aurait assez pour remplir 9 milliards de Link’s Awakening différents.

CEPENDANT, parmi les milliards de salles que l’on a dénombrée, il en existe un grand nombre qui sont injouables. Des salles qui ne ressemblent à rien ou n’ont aucun intérêt ludique. Des salles qui n’auraient pas leur place dans un jeu Zelda. Ni même dans un jeu tout court, en fait.

 

II. Affinons le calcul :

On va tenter d’améliorer notre dénombrement. On aimerait donc compter uniquement les salles qui sont traversables. C’est-à-dire les salles où toutes les entrées sont connectées entre elles.

Pour calculer ça, il n’existe pas de formules mathématiques. On va donc écrire un programme qui va tester toutes les possibilités. Malheureusement, ce n’est pas aussi simple que ça en a l’air.

 

Le premier réflexe serait de faire un programme qui regarde chaque salle une par une et vérifie qu’elle est traversable. Le problème c’est que c’est beaucoup trop long. L’ordinateur est extrêmement rapide mais pas assez. Imaginons qu’il puisse vérifier 100 000 salles par secondes, il lui faudrait tout de même 9000 ans pour finir son calcul. Et je n’ai pas spécialement envie d’attendre 9 millénaires pour publier cet article. Il faut donc trouver une autre solution.

 

La solution que j’ai choisie prend le problème dans l’autre sens. Puisque je veux pouvoir traverser la salle, je compte d’abord tous les chemins possibles qui passent par toutes les entrées. Je trace donc tous ces chemins, et pour chacun, je compte les cases qu’il traverse. Supposons qu’un chemin fasse 18 cases. Il reste alors 48-18=30 cases libres que l’on peut remplir comme on le souhaite. Ce qui fait donc 2³⁰ salles qui ont ce chemin. On sait avec certitude que ces 2³⁰ salles sont bien jouables car on a un chemin garanti entre toutes les entrées.

 

Grâce à ce programme bien plus rapide, on peut calculer le résultat en temps raisonnable. Par exemple, combien existe-t-il de salles qui ont une entrée à gauche et une entrée en haut, à votre avis ?

Il y en a 7 752 713 218 476. Soit près de 8000 milliards. Et on ne parle ici que des salles avec deux entrées perpendiculaires. Il faudrait compter les salles aux entrées face à face, et celles avec 1, 3 ou 4 entrées.
Si j’ai choisi les salles avec deux entrées, c’est que ce sont les plus nombreuses.

 

III. Conclusion :

Si jamais un Zelda Maker sort un jour, vous pouvez être sûr qu’on ne sera jamais à court de jeux à jouer. Imaginez vous bien qu’ici, nous avons simplifié le problème à l’extrême. Ajoutez les différentes cases, des salles de donjons plus grandes, des monstres, des objets du donjon, vous obtiendrez très vite un nombre énorme de possibilités. Il faut aussi considérer le fait qu’un donjon est constitué d’une vingtaine de salles. On peut donc, en théorie, concevoir bien plus de donjon de LA qu’il n’y a d’atomes dans l’univers. C’est vous dire si on peut en faire beaucoup !